Merge Sort

Merge Sort is one of the most popular methods of sorting an array and as offers a constant operating time of O(n \log(n)). And, as the name suggests it involves merging of several sorted arrays to combine and form a single sorted arrays in the end.

The steps involved in merge sort are:-

1. Divide the array in 2 parts left and right.
2. Now recursively divide the left and right parts into more left and right sub parts.
3. Keep doing step 2 , until the sub parts are no greater than a single element.
4. Once you have a single element, it becomes easy to compare.
5. Based upon which element is smaller combine them to form a tiny sorted array.
6. Keep on combining these tiny sorted array to form a new sorted array.
7. Repeat this step recursively to obtain a complete sorted array.

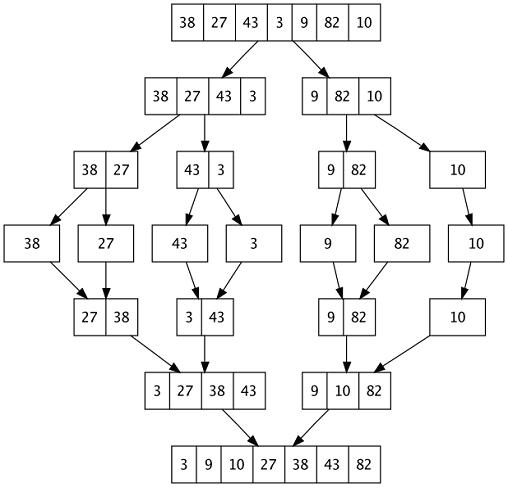
The image below will help to understand the concept more clearly:-

As we can see from the image, the array is split into 2 parts – left and right, which are then recursively split. This is done till we get a single element and then these are combined to form a complete sorted array.

To combine 2 sorted arrays we can use the method discussed in this post
– How to combine 2 sorted arrays ?

Merge Sort also uses a Divide and Conquer strategy and we can define the algorithm for it in this way. The basic idea behind this strategy is that we break the problem into smaller pieces and start solving them. As we solve these small problems, we can combine them and work our way towards the solution.

# split in half
m = n / 2

# recursive sorts
sort a[1..m]
sort a[m+1..n]

# merge sorted sub-arrays using temp array
 b = copy of a[1..m]
 i = 1, j = m+1, k = 1
 while i <= m and j <= n,
     a[k++] = (a[j] < b[i]) ? a[j++] : b[i++]
      → invariant: a[1..k] in final position
 while i <= m,
     a[k++] = b[i++]
      → invariant: a[1..k] in final positionCode language: PHP (php)

Implementation:

Here is the implementation of the above algorithm:-

#include<stdio.h>

//defining a function to merge 2 sorted arrays
//note that the 2 arrays will be contained in a single array
//as the left and right part
void merge(int arr[], int start, int mid, int end)
{
    // the array is as:- {start, ... ..mid, mid+1, .....end}
    // thus there are 2 arrays we need to merge

    //1st array , starting index and last index
    int i = start;
    int l1 = mid;

    //2nd array , starting index and last index
    int j = mid + 1;
    int l2 = end;

    //create an auxiliary array to store the elements
    int len = end - start + 1;
    int *arr2 = (int *)malloc(sizeof(int)*len);
    int k = 0;

    //apply the algorithm to merge 2 sorted arrays
    while(i <= l1 && j <= l2)
    {
        if(arr[i] < arr[j])
            arr2[k++] = arr[i++];
	else
	    arr2[k++] = arr[j++];
	}

        while(i <= l1)
            arr2[k++] = arr[i++];
	while(j <= l2)
	    arr2[k++] = arr[j++];

	//copy the auxiliary array to original array
	for(k = 0; k < len; k++)
	    arr[start++] = arr2[k];

	//free the memory
	free(arr2);
}

// a function to perform merge sort on an array with the given
// starting and ending index
void performMergeSort(int arr[], int start, int end)
{
    if(start < end)
    {
        //to get the middle of the array
	int mid = start + (end - start) / 2;

	//recursively dividing the left and right parts
	performMergeSort(arr, start, mid);  /* left part */
	performMergeSort(arr, mid+1, end);  /* right part */

	//finally we need to merge them
	merge(arr, start, mid, end);
    }
}

//defining a function to perform merge sort on array arr[] of given size
void mergeSort(int arr[], int size)
{
    performMergeSort(arr, 0, size-1);
}

// driver function to test the above function
int main(void)
{
    int i;
    int arr[10] = {2, 6, 4, 10, 8, 1, 9, 5, 3, 7};

    mergeSort(arr,10);

    printf("SORTED array:- ");
    for(i = 0; i < 10; i++)
        printf("%d ",arr[i]);

    return 0;
}
Code language: PHP (php)

Properties of MERGE sort:-

Time Complexity: O(n log(n)) for all cases
Space Complexity: O(n) for the auxiliary array
The code and test cases are available on Github.

Video Explanation: