Question: You are given an array of integers, and asked to find out two integers which sum up to a specific target. It can be assumed that there is only one solution.
Input:
arr [ ] = { 2, 7, 11, 15 }
target = 9Output:
[0, 1]
Let us try to understand the problem statement and its test cases first.
In this problem, an array is provided to you along with a target element. There exist only 2 elements in this array, which sum up to this target element. Given these conditions, we need to find the indices of these two elements.
Let us see some sample test cases:
#Case 1:
arr[] = { 2, 7, 11, 15 }, target = 9
Output: [ 0, 1 ]
Since, arr[0] + arr[1] == 9
(2) (7)
# Case 2:
arr[] = { 3, 2, 4 }, target = 6
Output: [ 1, 2 ]
arr[1] + arr[2] == 6
(2) (4)Code language: PHP (php)In each of the test cases, we can see that the sum of numbers reaches the target. Note that there can be only one possible solution, and we cannot use the same number twice.
This is a really popular interview question, as it can be solved in a lot of ways. Generally, the interviewer will keep on asking you more and more ways just to see your thought process. Let us look at the common ways to solve it.
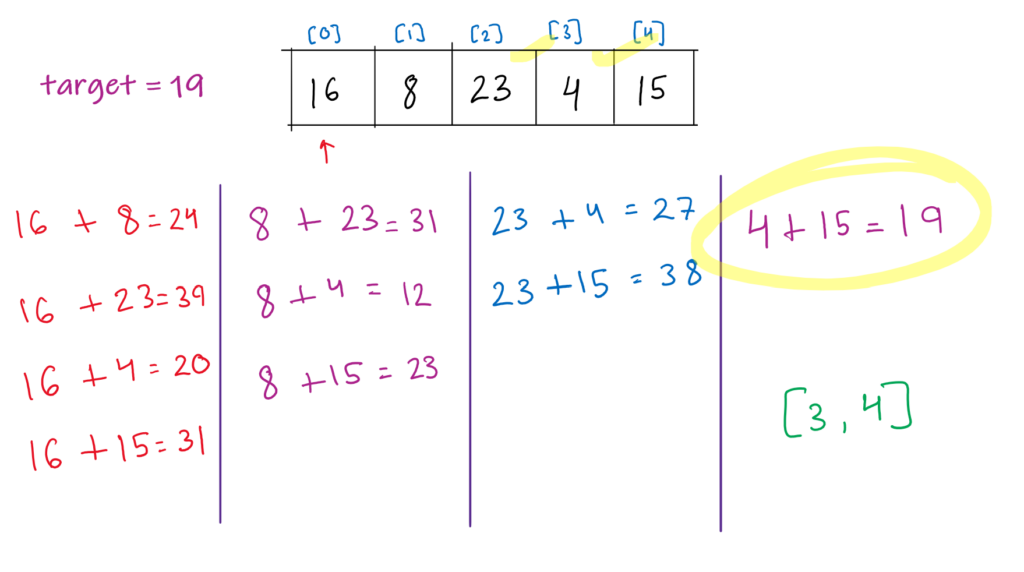
Method 1: Brute Force
A brute force solution to this problem would be:
- Start a loop that traverses each element of the array.
- Start an inner loop that again traverses each element of the array except the element selected from the first loop.
- Check if the sum of both the elements equal the target sum.
- If yes, return the indices.
This method would work flawlessly, but the only problem is the time taken by it to achieve the desired result. The time complexity of this approach is O(n^2), as we are traversing all the elements of the array two times.
Let us try to improve this approach. Usually, in questions where you have search, sorting goes hand in hand. Can we solve this using sorting?
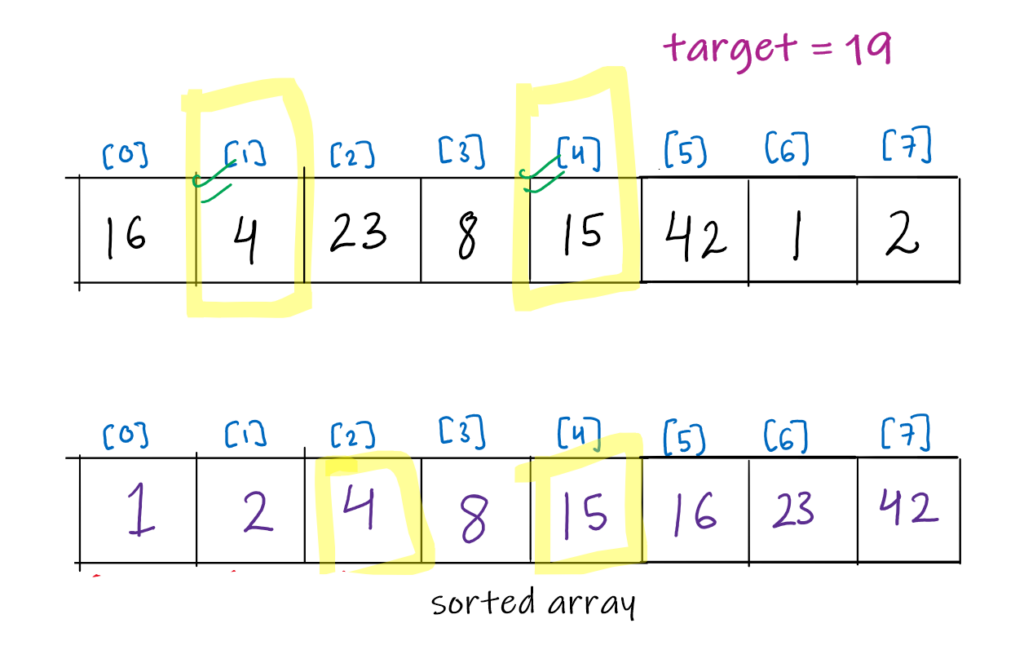
Method 2: Using Sorting
We can get some advantage if the array is already sorted. An approach to solve the problem would be:
- Sort the given array.
- Start two pointers. Pointer A starts from the beginning of the array, such that it points to the smallest element. Pointer B starts from the end of the array, pointing at the maximum element of the array.
- Now, start a while loop
while(pointer A < pointer B) - Get a sum of the elements at
pointerAandpointerB. - This is where the magic comes in. If the sum is less than
target, it simply means that we need to add a bigger number. Hence move thepointerAone step ahead. Else, we need a smaller number, and we can move thepointerBone step backward. - Somewhere along this iteration, we will get our desired indices.
int[] twoSumSorting(int[] nums, int target) {
int[] copyArray = Arrays.copyOf(nums, nums.length);
Arrays.sort(copyArray);
int head = 0;
int tail = copyArray.length - 1;
int num1 = 0, num2 = 0;
while (head < tail) {
int sum = copyArray[head] + copyArray[tail];
if (sum < target) {
head++;
}
else if (sum > target) {
tail--;
} else {
num1 = copyArray[head];
num2 = copyArray[tail];
break;
}
}
// Create the result array with indices
int[] result = new int[2];
for (int i = 0; i < nums.length; i++) {
if (nums[i] == num1) result[0] = i;
if (nums[i] == num2) result[1] = i;
}
return result;
}
Code language: Java (java)The above method works in a time complexity of O(n*\log n) because of the sorting step involved. You can use a quick sort algorithm to sort your array.
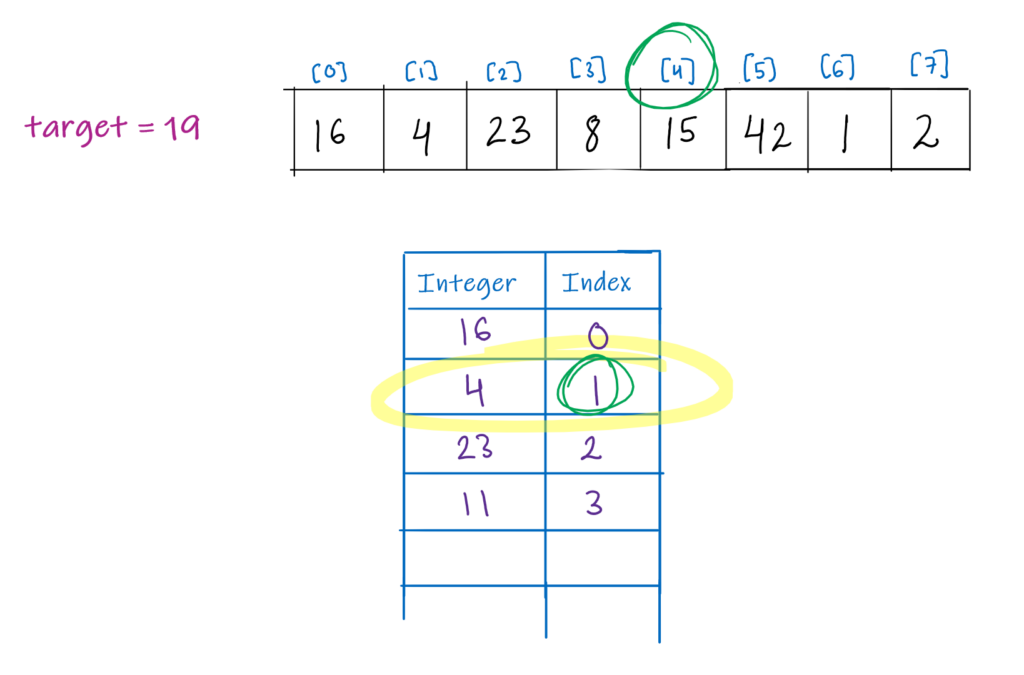
Method 3: Use Hashing
In the previous method, we did not use extra space and achieved a decent time complexity. But, if you can allow yourself to compromise on some space, you can solve this problem in an even efficient manner.
Instead of finding two numbers whose sum equal to a target value, we can think of the problem in an alternative way.
target\_value\ -\ first\_number\ =\ second\_number
So, we can develop an algorithm in the following way:
- Initialize a hash-table that will store the index and the element.
- Start to traverse the array.
- For each element in the array use the above define formula to find the complementing number.
- Look up the complementing number in the hash table. If found, return the
2indices. - Else, add the element along with its index to the hash table and proceed with the other elements.
Implementation:
int[] twoSumHashing(int[] nums, int target) {
// Create a HashMap
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
// Get the complement using the target value
int complement = target - nums[i];
// Search the hashmap for complement, if found, we got our pair
if (map.containsKey(complement)) {
return new int[]{map.get(complement), i};
}
// Put the element in hashmap for subsequent searches.
map.put(nums[i], i);
}
throw new IllegalArgumentException("No two sum solution");
}
Code language: Java (java)Time Complexity: O(n)
Space Complexity: O(n)
As always, the implementation for all the 3 methods and the corresponding test cases can be found on Github as well.
Video Explanation:



1 comment
Like the simplicity and explanation.
Comments are closed.