Binary Search

2K

Binary Search only works when your input list of elements is already sorted. This is main and the most important condition for this search algorithm. Unlike Linear Search, we take advantage of the sorted nature of the array. We always search in the middle portion of the array.

Working of Binary Search:

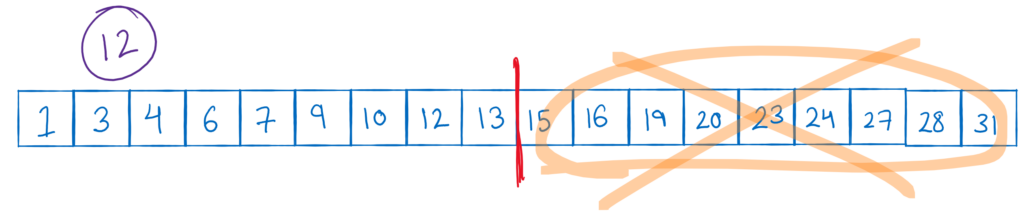
Let us say we have this sample array. Note that this array is sorted.

I want to search for the element 12 in this array. One way, I can proceed is by dividing the array in 2 halves. As soon as we break the array, you can see that we have a diversion between 13 and 15.

Note that we have to search for number 12. The right part of the array starts from 15. Because the array is sorted, you can easily conclude that all the elements in the right sub-array would be greater than my search query 12. So we can easily discard that part of the array. It is very likely, that we will find our result in the first part.

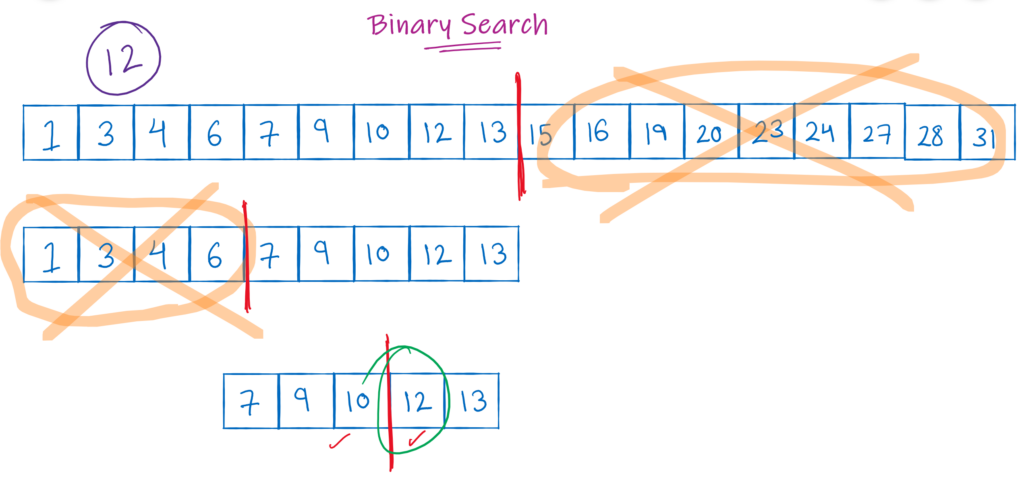
Once again, we can treat the first half of the array as a problem in itself. We can again divide it in 2 halves.

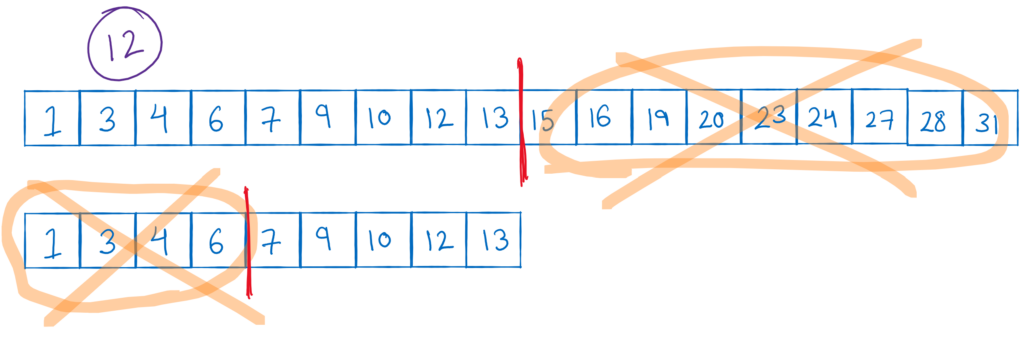
As soon as we divide the left sub-array in 2 parts, we see the elements 6 and 7 at the divider. Since 12 is greater than 6, we can safely discard the left part of this sub-array. I hope this is now giving you an idea about how this technique works.

If you keep on repeating this process, eventually you will come at a division, where you can reach the desired element 12.

The algorithm therefore would look something like:

1. Set the start position as beginning of array.
2. Set the end position as the end of array.
3. Start a loop
4. Check the middle element. If it matches, we found our result.
5. If (middle element > number to search), update the end position to mid.
6. Else, update the first position.
7. Repeat steps 4–6 until we find our element, or exhaust out of options.

Real life example:

Suppose you want to search a word in a dictionary. What we do is we directly go to some approximate page [say, middle page] and start searching from that point. If the word that we are searching is at the middle page, then we are done with the search.

However, if the alphabet is before the selected page then we apply the same process for the first half otherwise apply the same process to the second half.

So in a way we are again applying binary search, as we are dividing the problem into 2 halves. This is also known as the divide and conquer algorithmic paradigm.

Implementation:

  static boolean binarySearch(int[] arr, int numberToSearch) {

    int left = 0;
    int right = arr.length - 1;

    while (left <= right) {

      // Find the mid index
      int mid = (left + right) / 2;

      // Check at mid index
      if (arr[mid] == numberToSearch)
        return true;

      // Update the terminal indices
      if (arr[mid] < numberToSearch) {
        left = mid + 1;
      } else
        right = mid - 1;
    }

    return false;
  }
Code language: Java (java)

Time Complexity: O( \log n)
Space Complexity: O(1)

The code and test cases can be found on GitHub.

Video Explanation: