Question: Given 3 arrays, where each element represent the height of a cylinder. Find the maximum possible height of equal stacks by removing one or more cylinders from the original stack.
Example:
Input:
n1[] = {3, 2, 1, 1, 1}
n2[] = {4, 3, 2}
n3[] = {1, 1, 4, 1}Output: 5
Problem Statement
Let us try to simplify the problem statement first.
The problem states that you are provided with 3 sets of arrays. Each element in the array represents the height of a cylinder. Now, all these cylinders are absolutely identical except their height. So as per the input test case, you have the cylinders like:
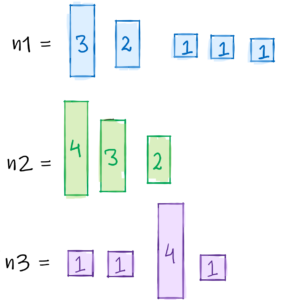
Now, these cylinders are to stacked on top of each other. Once they are stacked, they would start to look like:
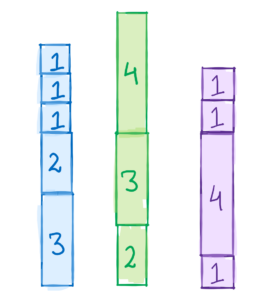
The problem now says that you can remove one or more cylinders from one or more stacks. The end goal of removing cylinders is that you should have equals stacks, i.e. the three stacks should be of the same height. To find the solution we need to maximize this height and that should be the answer to this problem. In this test case, the answer would be 5 after we have removed the respective cylinders.
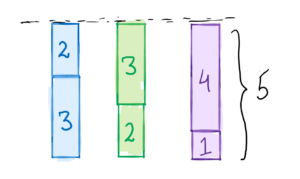
Brute Force Method:
A brute force method wouldn’t actually help to solve this problem very much. But still it will help you to start thinking about the solution to the problem. What we can do is, we can try to remove the first cylinder from the first stack, and check if the heights of all the 3 stacks are now same. If yes, we have reached our answer.
If not, try to remove a cylinder from the second stack and again verify. So the Brute Force algorithm would look like:
- Remove a cylinder from a stack.
- Check if the heights are equal.
- If yes, we have reached the solution.
- If not, choose a different stack and remove a cylinder.
- Once you have tried to remove
1cylinder, follow steps1-4with2cylinders this time, and then with3and so on.
You would realize that eventually you would reach the answer, but it wouldn’t be an efficient approach. That is because there are a lot of combinations possible and you possibly can’t iterate over all of them in a fast manner.
Efficient Way
Instead of trying to remove one cylinder at a time, and then finding the height of all the cylinders, we can take advantage of the Stack data structure. We can create 3 new stacks with the cumulative sums of the cylinder heights in each stack. This way the top element of each stack would tell you the current height of the stack.
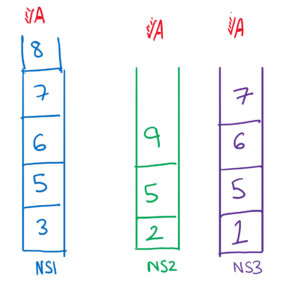
Once, we have these stacks, you can now try to remove the top element from the highest stack. This seems intuitive too, because if you are trying to achieve equal stacks, you would want to reduce the height of the highest stack first.
Now, you can go on removing the highest element from each of the 3 stacks until the top element of all the stacks is same. If the top element is same it would mean that the heights will also be same and hence equal.
Code:
public int equalStacks(int[] h1, int[] h2, int[] h3) {
int maxHeight = 0;
Stack<Integer> st1 = new Stack<>();
Stack<Integer> st2 = new Stack<>();
Stack<Integer> st3 = new Stack<>();
fillStacks(st1, h1, st2, h2, st3, h3);
// Run a loop until every stack has at-least 1 element
while (!st1.isEmpty() && !st2.isEmpty() && !st3.isEmpty()) {
int stack1Height = st1.peek();
int stack2Height = st2.peek();
int stack3Height = st3.peek();
// If all stacks are of same height, just return the height
if (stack1Height == stack2Height && stack2Height == stack3Height) {
maxHeight = st1.peek();
break;
}
// Else find the stack with maximum height and remove the block
if (stack1Height >= stack2Height && stack1Height >= stack3Height) {
st1.pop();
} else if (stack2Height >= stack1Height && stack2Height >= stack3Height) {
st2.pop();
} else if (stack3Height >= stack1Height && stack3Height >= stack2Height) {
st3.pop();
}
}
return maxHeight;
}
private void fillStacks(Stack<Integer> st1, int[] h1, Stack<Integer> st2, int[] h2, Stack<Integer> st3, int[] h3) {
int st1TotalHeight = 0, st2TotalHeight = 0, st3TotalHeight = 0;
// pushing consolidated height into the stack instead of individual cylinder
// height
for (int i = h1.length - 1; i >= 0; i--) {
st1TotalHeight += h1[i];
st1.push(st1TotalHeight);
}
for (int i = h2.length - 1; i >= 0; i--) {
st2TotalHeight += h2[i];
st2.push(st2TotalHeight);
}
for (int i = h3.length - 1; i >= 0; i--) {
st3TotalHeight += h3[i];
st3.push(st3TotalHeight);
}
}
Code language: Java (java)Time Complexity: O(n1 + n2 + n3)
Space Complexity: O(n1 + n2 + n3) for the 3 new stacks that we create.
You can find the code and test cases on Github.
Problem statement on HackerRank.
Video Explanation:


