The TREE Data Structure

A tree is a data structure similar to a linked list but instead of each node simply pointing to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of a non-linear data structure. A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.

In trees ADT (Abstract Data Type), order of the elements is not important. If we need ordering information, linear data structures like linked lists, stacks, queues etc can be used.

Some of the important information associated with a tree data structure are:-

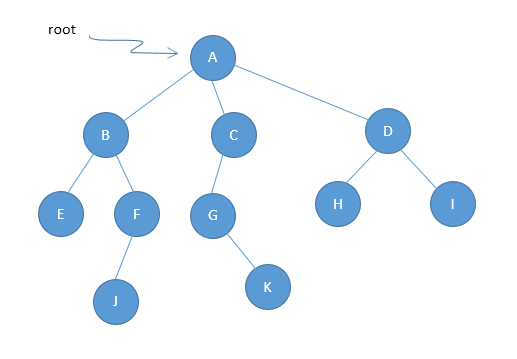
• The root of a tree is the node with no parents. There can be at most one root node in a tree (node A in the above example).
• An edge refers to the link from parent to child (all links in the figure).
• A node with no children is called a leaf node (E, J, K, H and I).
• Children of same parent are called siblings (B, C, D are siblings of A and E, F are the siblings of B).
• A node p is an ancestor of a node q if there exists a path from root to q and p appears on the path. The node q is called a descendent of p. For example, A, C and G are the ancestors of K.
• The depth of a node is the length of the path form the root to the node (depth of G is 2, A – C – J).
• The height of a node is the length of the path from that node to the deepest node. A (rooted) tree with only one node (the root) has a height of zero. In the previous example the height of B is 2 (B – F – J).
• Height of the tree is the maximum height among all the nodes in the tree and depth of the tree is the maximum depth among all nodes in the tree. For a given tree depth and height returns the same value. but for individual nodes we may get different results.
• Size of a node is the number of descendants it has including itself (size of sub-tree C is 3).
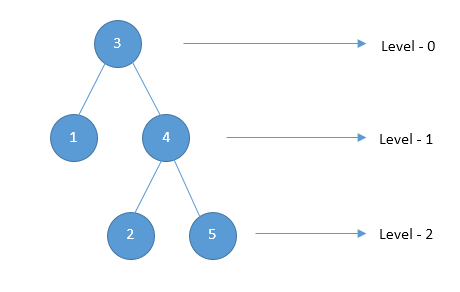
• Set of all nodes at a given depth is called level of the tree (B, C and D are same level). The root node is at level zero.
  
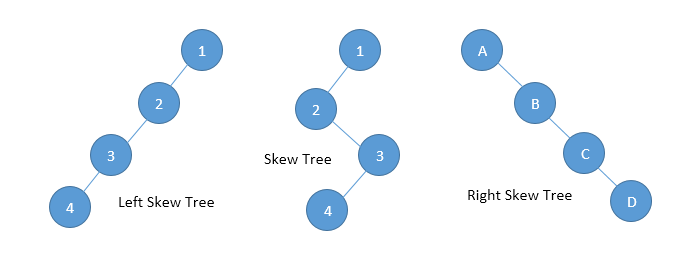
• If every node in a tree has only one child (except leaf node) then we call such a tree as skew tree. If every node has only left child then we call them as left skew trees. Similarly, if every node has only right child then we call them as right skew trees.