Give an algorithm to find the height(or depth) of a binary tree.

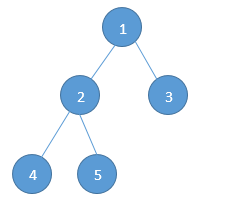
Question: Given the root pointer to a binary tree, find the height.

Input: Sample Tree (Pointer to node 1 is given).
Output: 3

The method we will learn relates to the same method we discussed in the post how to find the size of a binary tree –

• Find the size of a binary tree

In the above post we applied a recursive approach because the tree follows a recursive property. Every node has the same property. It has a root value, a left pointer and a right pointer. This is seen in the left sub-tree and right sub-tree as well.
The depth of the binary tree is the height of the tree, or we can say the number of levels in the binary tree. In the above tree we have 3 levels.

If we see the first node, we have a property:- max (left height, right height) + 1

So, what we can do is we can recursively calculate the height of left sub-tree and right sub-tree of a node and assign height to the node as max of the height of two children + 1. This is also similar to PreOrder Traversal.

#include<stdio.h>

struct binaryTreeNode{
	int data;
	struct binaryTreeNode * left;
	struct binaryTreeNode * right;
};

int heightOfBinaryTreeRecursive(struct binaryTreeNode * root)
{
	// Initialize 2 variables for left and right height
	int leftHeight;
	int rightHeight;
	
	// The terminating case
	if(root == NULL)
		return 0;
	else
	{
		// Find the depth of left sub-tree
		leftHeight = heightOfBinaryTreeRecursive(root -> left);
		
		// Find the depth of right sub-tree
		rightHeight = heightOfBinaryTreeRecursive(root -> right);
		
		// Compare the two heights and return the larger of two + 1
		if(leftHeight > rightHeight)
		{
			// Return the leftHeight + 1
			return (leftHeight + 1);
		}
		else
		{
			// Return the rightHeight + 1
			return (rightHeight + 1);
		}
	}
}

Time Complexity:- O(n)
Space Complexity:- O(n)