Counting Sort

2K

Counting sort is not a comparison sort algorithm. The sorting techniques that work on comparison are:

• Selection Sort
• Bubble Sort
• Insertion Sort
• Merge Sort
• Quick Sort

The best time complexity you can achieve in any of these sorting techniques is O(n * \log(n)). However, is some very specific cases, you can achieve an even faster computation time of O(n). This is made possible by an assumption. We assume that the input data set is within a finite limit.

For example, if you want to sort some characters of the English alphabet. You know that there can be a maximum of 26 characters. Similarly, if you are trying to sort marks of some students, and you know that they can range only between 0-100. These are the cases where Counting Sort can come in very handy.

Basic Idea:

The basic idea of counting sort is to determine, for each input element X, the number of elements smaller than X. This information can be used to place the element directly into its correct position in the resultant sorted array. For example, if there are 10 elements less than X, then X would belong at position 11 in the output array.

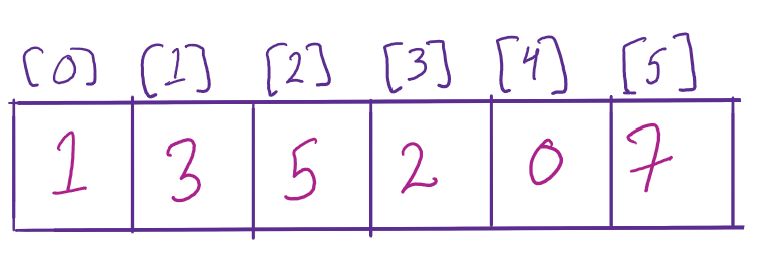
In the below example, arr[0..n – 1] is the input array with length n. In counting sort we need two more arrays: let us assume array count[0..n – 1] as another array and out[0..n – 1] as the final sorted array.

• Determine the range of given input elements by doing a single scan.

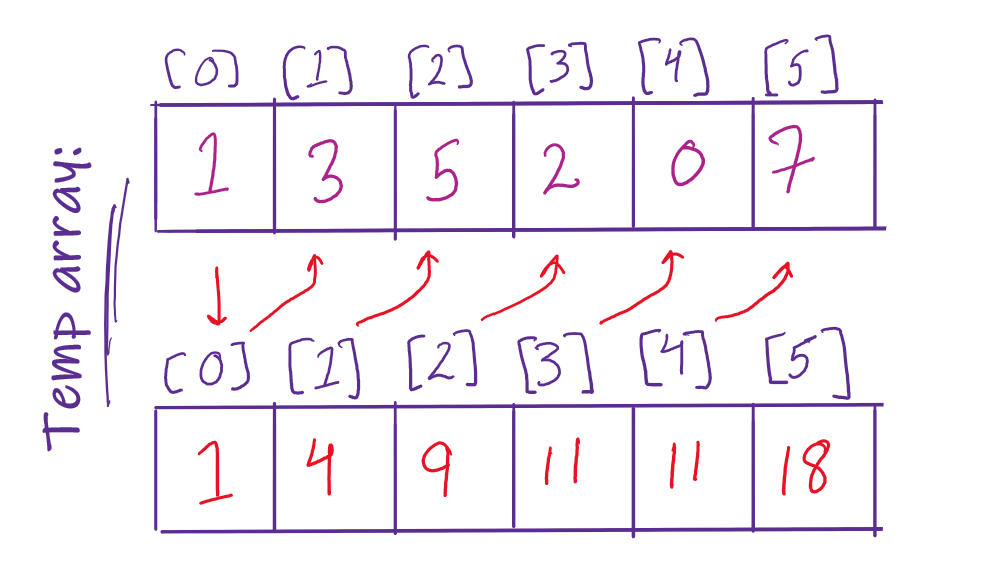
• Count the occurrences of each of the element and store it in an auxiliary array.

• Perform a cumulative sum on the elements of this new array.

• Use this auxiliary array to place the original elements in place. Example: temp[2] would indicate the position of 2 in the final output array. With a 0 based indexing, 2 would go at position number 8. Repeat this process for every element of the input array.

Implementation and Code:

Here is an implementation of the algorithm:-

static void countingSort(int[] arr)
{
  int max = Arrays.stream(arr).max().getAsInt();
  int min = Arrays.stream(arr).min().getAsInt();
  int range = max - min + 1;

  // Auxiliary array to store counts of each element
  int[] count = new int[range];

  // Auxiliary array to store the resultant sorted array
  int[] output = new int[arr.length];

  // Store count of each element
  for (int j : arr) {
    count[j - min]++;
  }

  // Change count[i] so that count[i] now contains actual
  // position of this character in output array
  for (int i = 1; i < count.length; i++) {
    count[i] += count[i - 1];
  }

  // Build the output array
  // To make it stable we are operating in reverse order.
  for (int i = arr.length - 1; i >= 0; i--) {
    output[count[arr[i] - min] - 1] = arr[i];
    count[arr[i] - min]--;
  }

  System.arraycopy(output, 0, arr, 0, arr.length);
}
Code language: Java (java)

Time Complexity: O(n)
Space Complexity: O(n + k) where k is the range of the elements.

You can also find the sample code along with test cases on GitHub.

Video Explanation: