[Hackerrank] – Equal Solution

Let us try to understand this problem statement first. It is actually very verbose. We will try to simplify it as much as possible. Christy wants to give chocolates to her colleagues, and at the same time tries to ensure that everyone has equal chocolates at the end. To achieve this she either gives 1,2, or 5 chocolates to everyone except any one individual.

Every-time she does this, it is counted as 1 operation. We need to make sure that Christy can achieve this task in the minimum number of steps possible.

Look at one of the sample test cases

Input:
arr = [1, 1, 5]

Explanation:
Operation 1: Give 2 chocolates to everyone except employee 3
=> [3, 3, 5]

Operation 2: Give 2 chocolates to everyone except employee 3
=> [5, 5, 5]

Hence answer = 2

Output:
2

Simplification of Problem:

Before starting to solve the problem, we can simplify it a little bit.

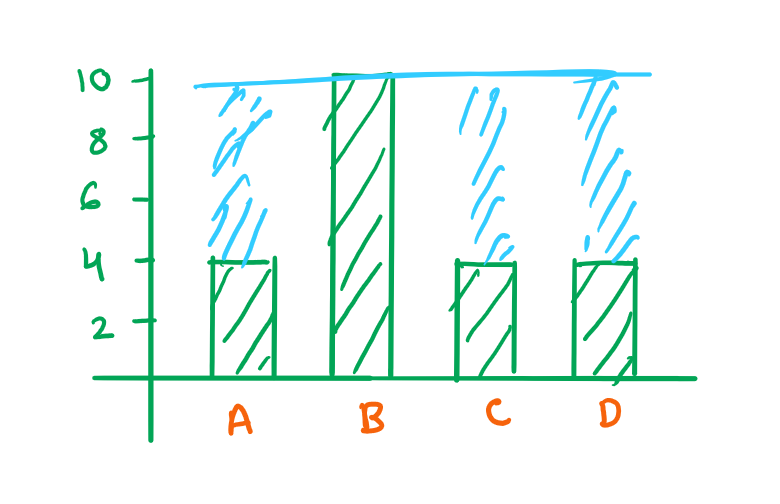
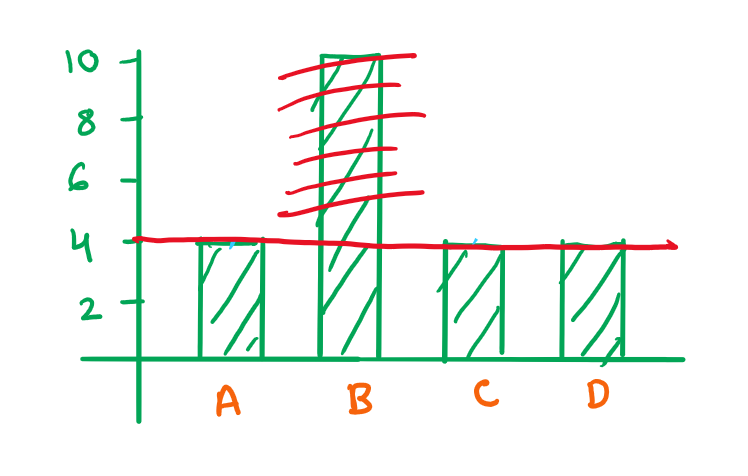
For example, let us say the current distribution is [4, 10, 4, 4]. One way to make the distribution equal is to give 6 chocolates to everyone except employee B. So we are giving chocolates to everyone except 1.

On the other hand, what if we try something else and do a reverse operation. This time, we take 6 chocolates only from employee B. We are again able to make the distribution equal for all the employees. So we are taking chocolates from only 1 employee.

These both operations are same. Upon a close analysis it can be concluded that:

giving\ chocolates\ to\ everyone\ except\ 1 \newline
=\newline
taking \ chocolates\ from\ only\ 1

Solution:

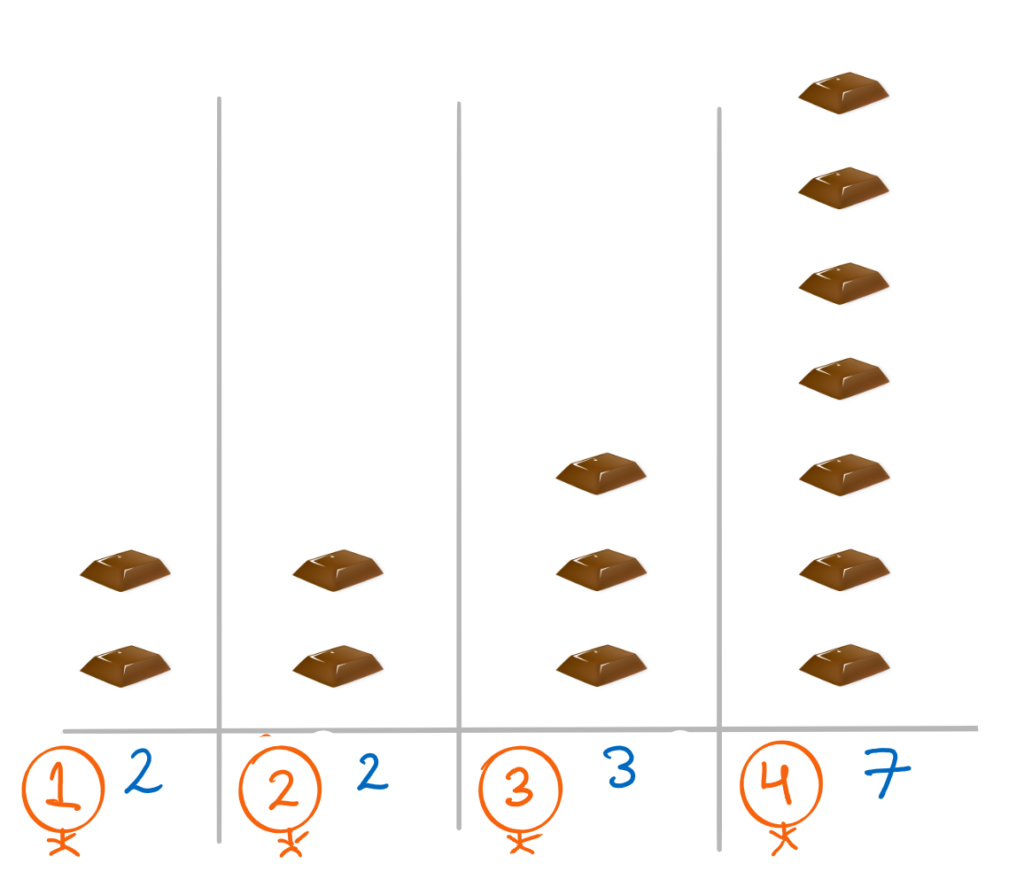
From the above simplification, it becomes easy to just make changes to one value in the array rather than changing all the values. Now we can start to solve the problem. Let us say the initial distribution is [2, 2, 3, 7]. First, let’s see a proof that the above simplification works.

Now we perform 2 operations side by side:
– Operation 1: Take 5 chocolates from only employee 4 <=> Give everyone 5 chocolates except employee 4

This changes the distribution to [2, 2, 3, 2] and [7, 7, 8, 7] respectively.

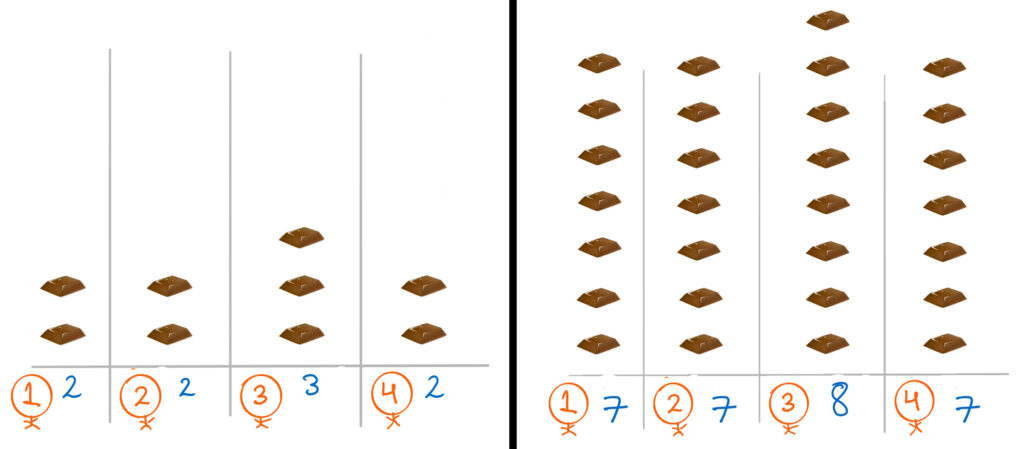
The second operation would look like:
– Operation 2: Take 1 chocolate from only employee 3 <=> Give everyone 1 chocolate except employee 3

This changes the distribution to [2, 2, 2, 2] and [7, 7, 8, 7]

Notice that although the quantities of chocolates are not same, the distribution is equal in both the cases.

How to Solve?

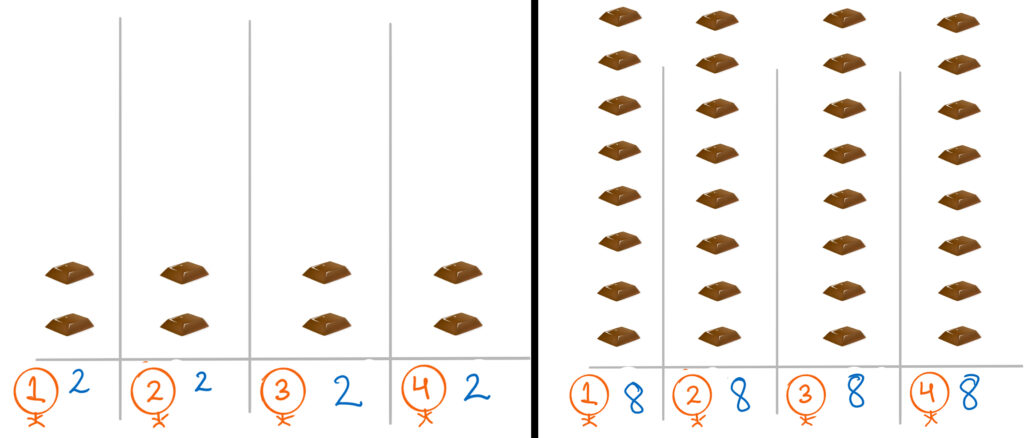
Now, to solve this problem let us take up a case where the distribution is: [2, 6, 6, 6]

One hint that we get from the above simplification is that we need to make the quantity equal to the lowest number possible. This way we can bring every employee to the same level. We start from the employee that has the highest number of chocolates and take either 1, 2, or 5 at a time. Each time we take chocolates, it counts as an operation.

#1: Take 2 chocolates from employee 2. This will count as 1 operation.

#2: Take 2 more chocolates from employee 2. This will again count as 1 operation.

Thus in 2 operations the distribution will change to [2, 2, 6, 6].

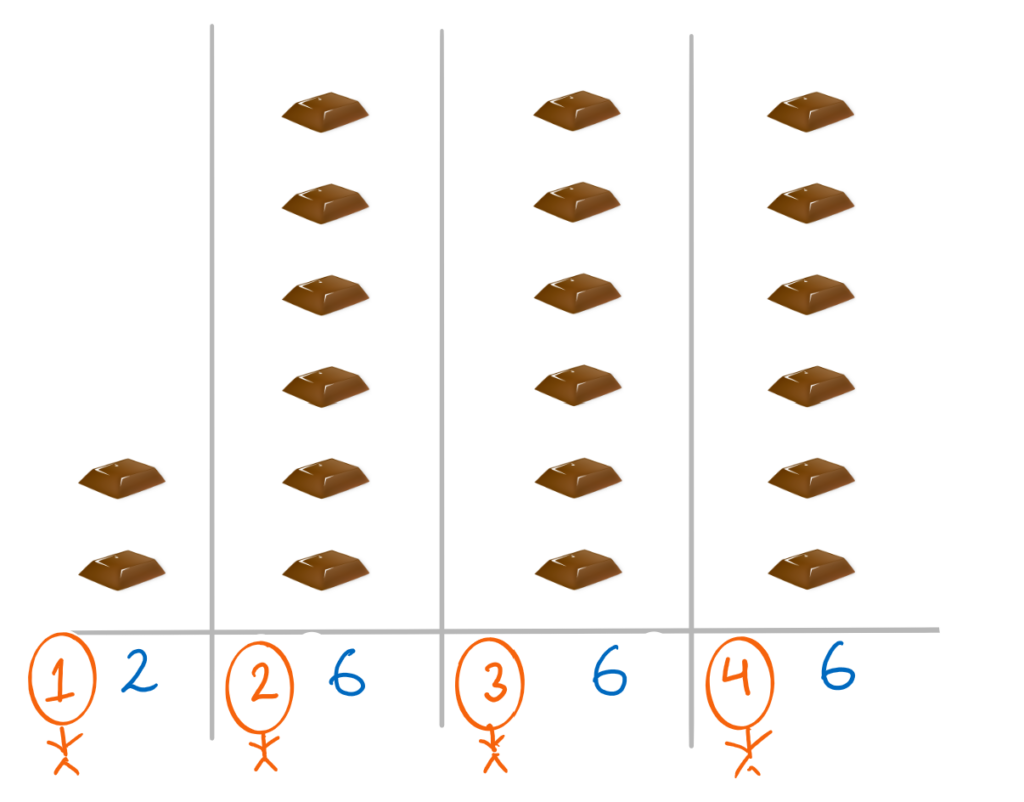
#3: Moving further ahead in the array, we see that the next employee again has 6 chocolates. This would again mean 2 operations.

#4: Employee 4 would also take up 2 operations.

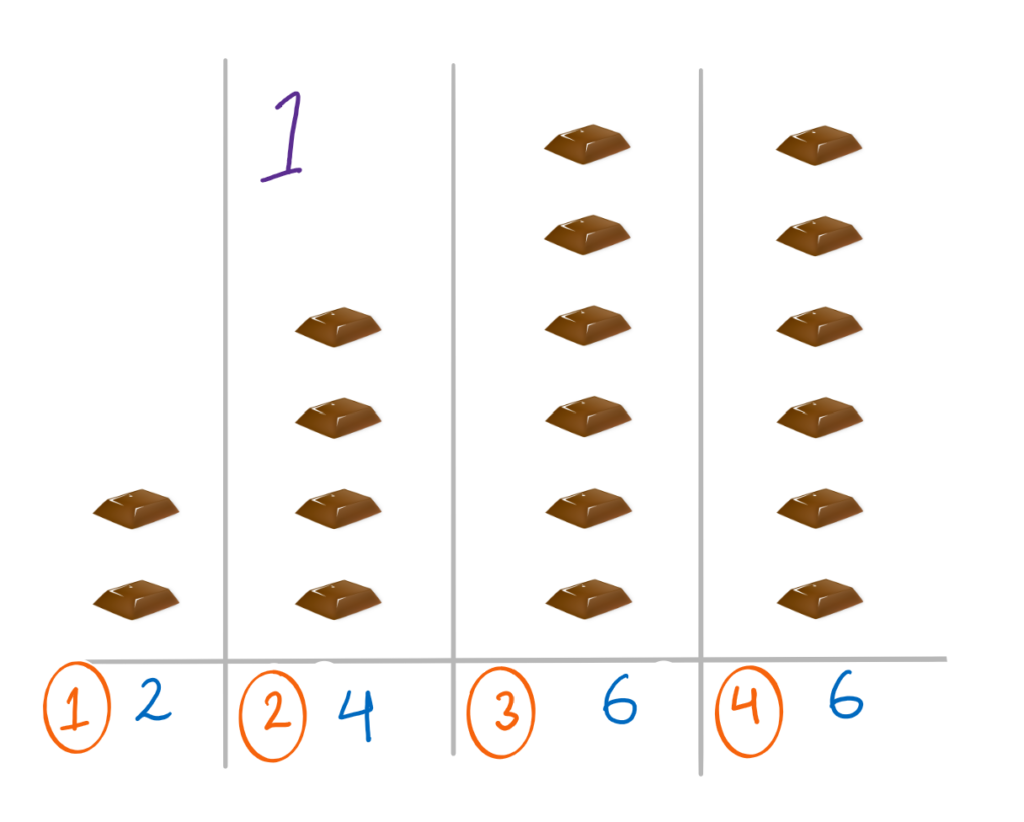
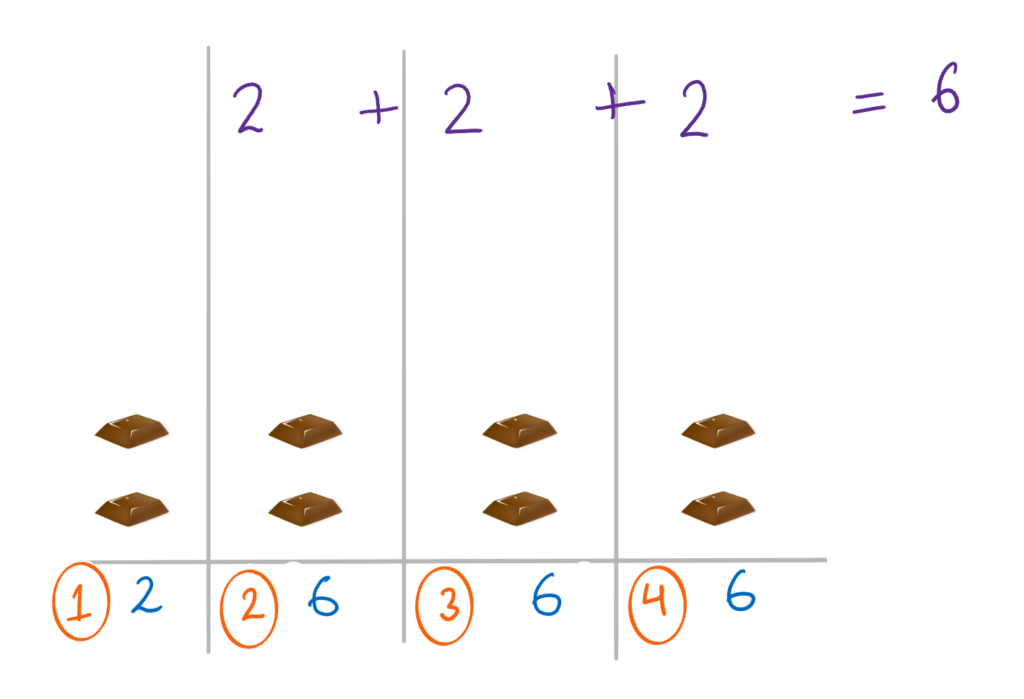
Ultimately, we have an equal distribution of [2, 2, 2, 2]. We are able to achieve this in a total of 6 operations and hence 6 is our answer.

An important point to note here is that we need to check for a range of minimum chocolates. min to min - 4. Where min is the initial minimum value in the array. Sometimes, you could get smaller number of operations with that range.

Code:

  int equal(int[] arr) {

    // Store all the possibilities
    int[] possibilities = new int[5];

    // Start with the minimum element
    int minimum = Arrays.stream(arr).min().getAsInt();

    for (int i = 0; i < possibilities.length; i++) {

      for (int k : arr) {
        int diff = k - minimum;
        int stepsRequired = diff / 5 + (diff % 5) / 2 + ((diff % 5) % 2) / 1;
        possibilities[i] += stepsRequired;
      }
      minimum--;
    }

    // Return the minimum number out of all the possibilities
    return Arrays.stream(possibilities).min().getAsInt();
  }
Code language: Java (java)

Time Complexity: O(n)
Space Complexity: O(1)

The code and test cases are also available on Github.

Video Explanation: