Question: Given the root pointer to a binary tree, find its size.
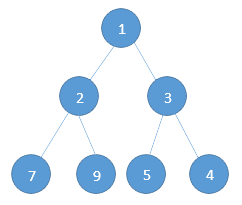
Input: Sample Tree (Pointer to node 1 is given). Find the size
Output: Size = 7
The size of the binary tree is basically the number of nodes in a binary tree. Since, the tree follows a recursive approach we can easily solve this problem by recursion. We calculate the size of left and right sub-tree recursively, add 1 (current node) and return to its parent.
The recursive implementation can be done as:-
#include<stdio.h>
struct binaryTreeNode{
int data;
struct binaryTreeNode * left;
struct binaryTreeNode * right;
};
// Recursive method to find the size of binary tree
// Finding the number of nodes
int sizeOfBinaryTreeRecursive(struct binaryTreeNode * root)
{
if(root == NULL)
return 0;
else
{
// We recursively travel the left sub-tree
// Add 1 for the root nodes
// We then recursively travel the right sub-tree
return (sizeOfBinaryTreeRecursive(root -> left)
+ 1
+ sizeOfBinaryTreeRecursive(root -> right));
}
}
EXPLANATION
CASE 1 :
When the root is null, it simply returns 0, because no nodes are present in tree.
if(root == NULL)
return 0;
CASE 2 :
Now let us take a case when only 1 node is present.
The else block executes
return (sizeOfBinaryTreeRecursive(root -> left)
+ 1
+ sizeOfBinaryTreeRecursive(root -> right));
This happens in the statement:-
- root -> left is NULL in this case and from above CASE 1 it will return = 0
- add 1
- root -> right is NULL again and from above CASE 1 it will return = 0
So the statement will return = 0 + 1 + 0
Hence, the size of the tree = 1
CASE 3 :
Taking a case of 1 node and left sub-tree.
Now when the command is executed
sizeOfBinaryTreeRecursive(root -> left)
The left sub-tree comes into consideration and we have the root pointer as -> 2
And from the above case we know that this tree will return a value of = 1
So, now we again have:-
- root -> left is sub-tree in this case and from above CASE 2 it will return = 1
- add 1
- root -> right is NULL again and from above CASE 1 it will return = 0
So, the statement will return = 1 + 1 + 0
Hence, the size of tree = 2
CASE 4 :
Taking the generalized case of 3 nodes, root left sub-tree and right sub-tree.
Now we simply have a right sub-tree as well.
- root -> left is sub-tree in this case and from above CASE 2 it will return = 1
- add 1
- root -> right is a sub-tree which will be similar to above CASE 2 and return = 1
So, the statement will return = 1 + 1 + 1
Hence, the size of the tree = 3
Thus, from the visualization of the above algorithm we can see that because of the repeating property of tree structure, size of tree can be calculated.
Time Complexity:- O(n)
Space Complexity:- O(n)
Method 2:- Find the size of the binary tree without using recursion.