We learned about the different type of traversals in this post
In pre-order traversal, each node is processed before (pre) either of its sub-trees. This is the simplest traversal to understand. However, even though each node is processed before the sub-trees, it still requires that some information must be maintained while moving down the tree. Let us consider an example
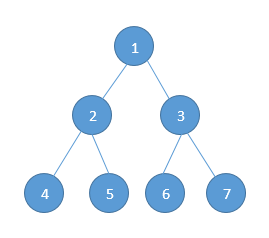 In the example tree shown above, the node “1” is processed first, then the left sub-tree, followed by the right sub-tree. Therefore, processing must return to the right sub-tree after finishing the left sub-tree. To move to right sub-tree after processing left sub-tree, we must maintain the root information. The obvious ADT (Abstract Data Type) for such information is a stack. Because of its LIFO (Last In First Out) structure, it is possible to get the information about the right sub-trees back in the reverse order.
In the example tree shown above, the node “1” is processed first, then the left sub-tree, followed by the right sub-tree. Therefore, processing must return to the right sub-tree after finishing the left sub-tree. To move to right sub-tree after processing left sub-tree, we must maintain the root information. The obvious ADT (Abstract Data Type) for such information is a stack. Because of its LIFO (Last In First Out) structure, it is possible to get the information about the right sub-trees back in the reverse order.
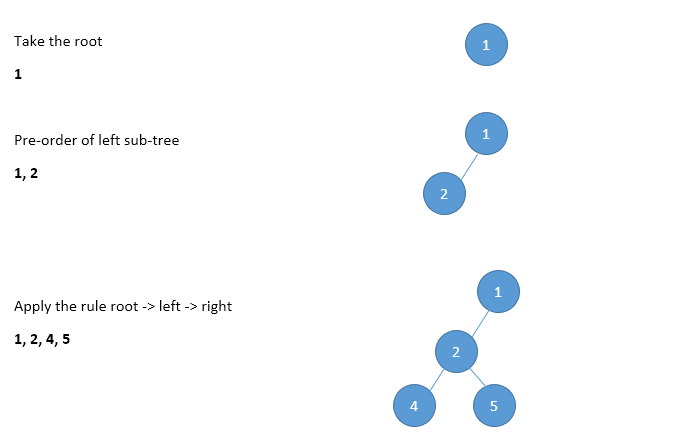
Pre-order traversal is defined as follows:
- Visit the root (Step 1)
- Traverse the left sub-tree in Pre-order (Step 2)
- Traverse the right sub-tree in Pre-order (Step 3)
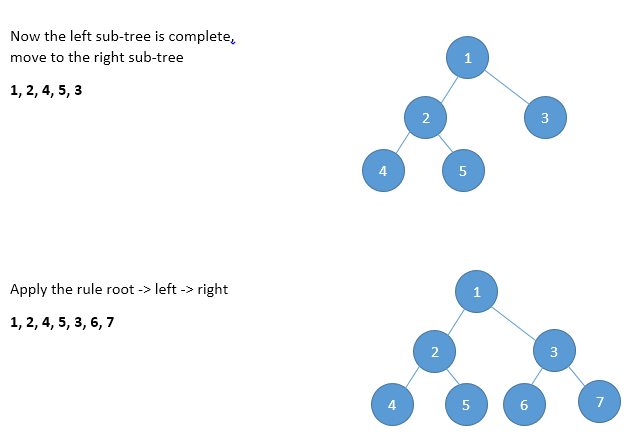
With this definition, let us try to traverse the above tree –
So the final pre-order traversal will be 1, 2, 4, 5, 3, 6, 7
We can therefore write the recursive version of the traversal as:-
void preOrderRecursive(struct binaryTreeNode * root)
{
if(root)
{
// Visit the root (Step 1)
printf("%d", root -> data);
// Preorder traversal of left sub-tree (Step 2)
preOrderRecursive(root -> left);
// Preorder traversal of right sub-tree(Step 3)
preOrderRecursive(root -> right);
}
}
Non-Recursive Preorder traversal
In recursive version a stack is required as we need to remember the current node so that after completing the left sub-tree we can go to right sub-tree. To simulate the same, first we process the current node and before going to left sub-tree, we store the current node on stack. After completing the left sub-tree processing, pop the element and go to its right sub-tree. Continue this process until stack is non-empty.
void preOrderNonRecursive(struct binaryTreeNode * root)
{
// Create a new stack
struct stackNode * S = null;
// We need to keep running the loop until stack is not empty
while(1)
{
while(root)
{
// Process the current node (Step 1)
printf("%d", root -> data);
S = push(S, root -> data);
// If left sub-tree exists, we need to add it to the stack.
// So go to the left tree (Step 2)
root = root -> left;
}
// If the stack is empty, that means all nodes have been traversed
// we need to break
if(isStackEmpty(S))
{
break;
}
// If stack is not empty, we need to see the last element in the stack
// So pop it
root = top -> data;
//Remove the element from stack
S = S -> next;
// Now go to the right sub-tree (Step 3)
root = root -> right;
}
// We need to delete the stack
free(S);
}
Time Complexity:- O(n)
Space Complexity:- O(n)
You can download the complete working code here.